Maths : 2 trucs simples pour la réussite de tous les enfants

Jo Boaler est professeur en sciences de l’éducation à l’université de Stanford. Elle a écrit le livre Experiencing School Mathematics. Elle affirme que seules deux choses simples suffiraient à assurer la réussite de tous les enfants en maths :

1. utiliser le pouvoir des croyances positives,
2. rendre les maths vivantes et visuelles.

 

1. Le formidable pouvoir des croyances positives

Jo Boaler explique que le cerveau des personnes qui ont un état d’esprit en développement grossit plus suite à une erreur que celui des personnes qui ont un état d’esprit fixe. L’état d’esprit en développement permet d’aborder les erreurs de manière positive et d’en tirer des leçons efficaces.

Ce qu’on apprend est lié à nos croyances : quand on croit qu’on a un potentiel d’apprentissage illimité, on apprend beaucoup plus (c’est ce qu’ont montré des IRM du cerveau d’élèves). Littéralement, plus de connexions se font entre les neurones !

L’instauration d’un état d’esprit en développement permet aux enfants de croire qu’ils pourront apprendre ce qu’ils veulent, qu’ils peuvent compter sur leur cerveau et leurs efforts.

>>>Pour aller plus loin :

7 clés pour instaurer l’état d’esprit de développement chez les enfants

Pourquoi est-il important d’expliquer la neuroplasticité aux enfants (et comment le faire) ?

 

2. La manière de poser les questions et les problèmes mathématiques : des fiches à la manipulation et à la visualisation

Jo Boaler propose d'”ouvrir” l’enseignement des mathématiques. Elle évoque plusieurs pistes à cet effet :

 

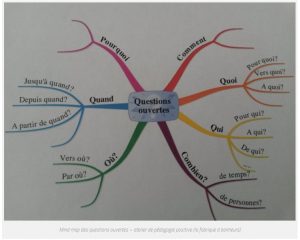
• poser des questions ouvertes

Les questions ouvertes admettent des réponses ouvertes (à la différence de oui ou non, d’un choix type QCM).

 

• aller au delà des questions sur les quantités, les opérations, les nombres, les calculs

Dans sa conférence Ted, Jo Boaler donne l’exemple d’un problème mathématique : il s’agit de retrouver la fonction qui donne le nombre de carrés dans la figure finale en fonction du nombre de carrés dans la figure de départ.

 

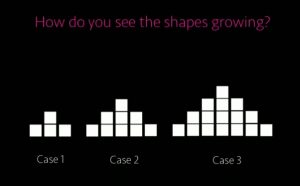
Plutôt que demander d’exprimer la fonction, Jo Boaler  a demandé : “Comment voyez-vous les formes grandir ?”. Elle a reçu autant de réponses différentes que d’élèves.

 

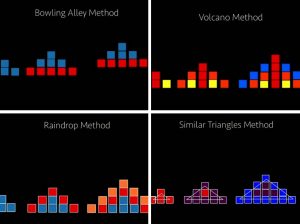
A force de manipulations, les élèves sont arrivés à se rendre compte que le ré-arrangement des petits carrés transforme les triangles en grand carré.

 

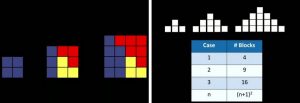
• enseigner les mathématiques de manière visuelle et créative

Jo Boaler insiste sur la manière de présenter les résultats : ajouter des couleurs, des schémas, des dessins…

 

• manipuler et arrêter de travailler sur des fiches/fichiers

Pour ma part, j’utilise un mix de différentes approches pour l’enseignement des mathématiques. Je ne peux plus me passer des bâtonnets numériques ni du boulier, j’utilise également beaucoup les multicubes avec les plus jeunes (maternelle/CP) et les attrimaths (notamment pour la géométrie).

 

Pour formaliser, je m’inspire de plusieurs méthodes :

• la méthode Lyons,
• la pédagogie Montessori,
• la pédagogie Reggio.

C’est ainsi par la combinaison de la méthode Lyons et des bâtonnets numériques que j’ai enfin compris pourquoi il y avait le mot “carré” dans racine carrée (… à 30 ans passés) !

 

• montrer la beauté et la richesse des maths

Le site MicMaths propose de nombreuses vidéos qui épateront les enfants : des tours de magie à base de formules mathématiques, des dessins et des mandalas à partir des tables de multiplication, des énigmes à résoudre…

Mickaël Launay essaie à travers ses vidéos de rendre les mathématiques moins abstraites et théoriques par une mise en pratique qui réconcilie plaisir de chercher et utilisation concrète des connaissances acquises.

 

• autoriser l’utilisation des doigts pour compter à tout âge

Jo Boaler cite les dernières découvertes en neurosciences :  empêcher l’utilisation des doigts pour compter serait néfaste au développement de l’esprit mathématique des enfants et des adolescents. Elle recommande de laisser les enfants utiliser leurs doigts aussi longtemps qu’ils en auront besoin, que ce soit à l’école ou à la maison (pour les devoirs).

 

• poser des « vrais problèmes » (et pas seulement des problèmes sur le papier) 

Quand on laisser les enfants construire le problème, ils ne se contentent pas de le résoudre, ils le formulent ! Quand le problème a un sens pour eux, ils sont plus enclins à manipuler, à agir, à regarder, à donner du sens, à faire des hypothèses, à discuter, à confronter les idées, à tester et à vérifier.

C’est ce qu’on retrouve dans les pédagogies type Freinet ou dans les apprentissages autonomes : les enfants résolvent des problèmes qu’ils rencontrent dans leur quotidien.

La posture de l’adulte est alors d’aider les enfants un peu moins, de les laisser réfléchir, chercher, se tromper et ajuster.