Tableau des critères de divisibilité des nombres entiers

Je vous propose un tableau qui résume les critères de divisibilité des nombres entiers courants jusqu’à 10, avec des exemples et des contre-exemples.

Télécharger tableau des critères de divisibilité au format PDF pour impression

Des critères existent pour savoir si un nombre est un multiple d’un autre nombre, c’est-à-dire pour savoir s’il est divisible par cet autre nombre, sans devoir poser une division.

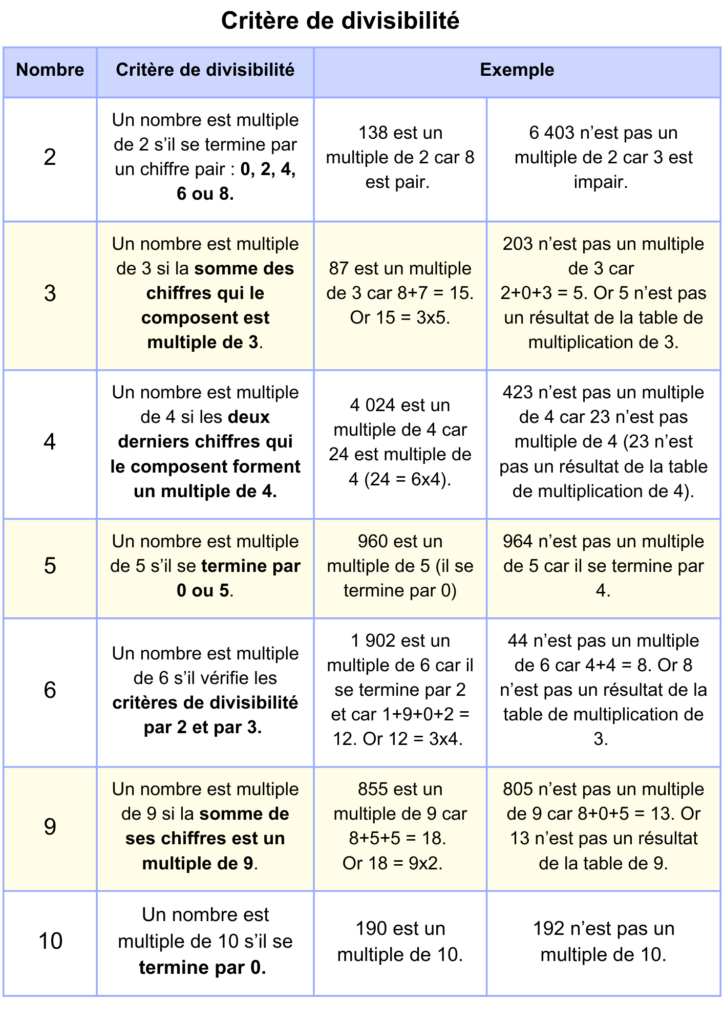
Un nombre est multiple de 2 s’il se termine par un chiffre pair : 0, 2, 4, 6 ou 8. 138 est un multiple de 2 car 8 est pair.

Un nombre est multiple de 3 si la somme des chiffres qui le composent est multiple de 3. 87 est un multiple de 3 car 8+7 = 15. Or 15 = 3×5.

Un nombre est multiple de 4 si les deux derniers chiffres qui le composent forment un multiple de 4. 4 024 est un multiple de 4 car 24 est multiple de 4 (24 = 6×4).

Un nombre est multiple de 5 s’il se termine par 0 ou 5. 960 est un multiple de 5 (il se termine par 0)

Un nombre est multiple de 6 s’il vérifie les critères de divisibilité par 2 et par 3. 1 902 est un multiple de 6 car il se termine par 2 et car 1+9+0+2 = 12. Or 12 = 3×4.

Un nombre est multiple de 9 si la somme de ses chiffres est un multiple de 9.855 est un multiple de 9 car 8+5+5 = 18. Or 18 = 9×2.

Un nombre est multiple de 10 s’il se termine par 0.190 est un multiple de 10.

………………………………………………

Si vous préférez une présentation sous forme de carte mentale, vous pouvez la retrouver dans cet article : Critères de divisibilité des nombres entiers