Multiplier des nombres relatifs : une carte mentale des règles de multiplication

Les nombres relatifs peuvent être multipliés entre eux. Il existe des règles à connaître pour la multiplication de deux nombres de signes contraires et la multiplication de deux nombres de mêmes signes. Multiplier des nombres relatifs, c’est multiplier leurs valeurs absolues (comme si les signes n’existaient pas), puis appliquer la règle des signes.

Télécharger la carte mentale pour multiplier des nombres relatifs au format PDF pour l’imprimer

Quand on multiplie des nombres relatifs par 0, le résultat est toujours 0.

Exemple : (−12) × 0 = 0 et (12) × 0 = 0

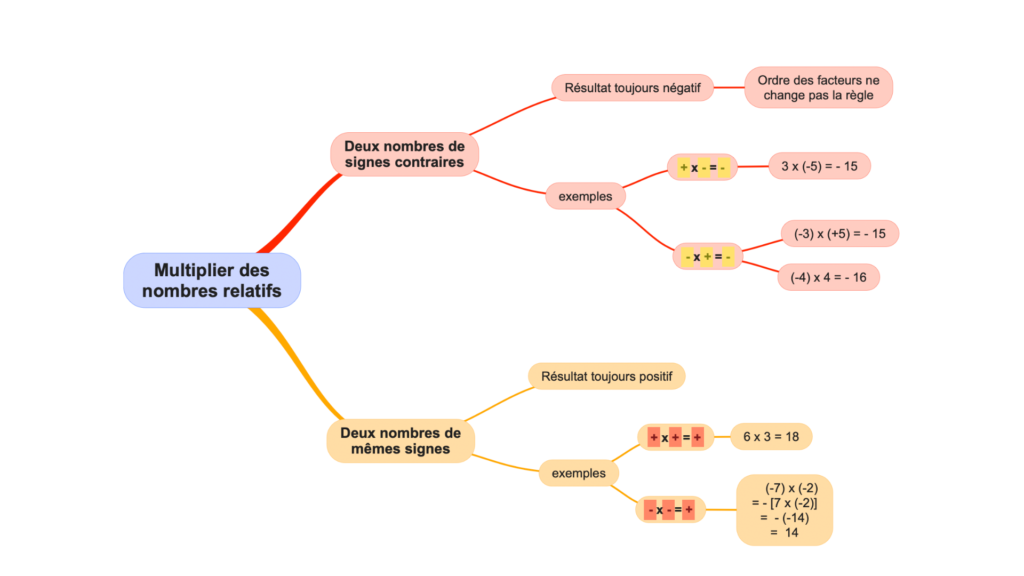
Deux nombres de signes contraires

Résultat toujours négatif : l’ordre des facteurs ne change pas la règle.

Exemples
+ x – = –
3 x (-5) = – 15

– x + = –
(-3) x (+5) = – 15
(-4) x 4 = – 16

Deux nombres de mêmes signes

Résultat toujours positif

Exemples
+ x + = +
6 x 3 = 18

– x – = +
(-7) x (-2)
= – [7 x (-2)]
= – (-14)
= 14

En résumé :

• Même signe → résultat positif
• Signes différents → résultat négatif 

$(-6)\times (-3)=18$ (négatif × négatif = positif)

7 × (−4) = −28 (positif × négatif = négatif)

(−3) × 7 = −21 (négatif × positif = négatif)

Exemples : 

(+5) × (+2)=+10

(−5) × (+2)=−10

(+5) × (−2)=−10

(−5) × (−2)=+10

 

Cas pour multiplier plusieurs nombres relatifs

Si on multiplie plusieurs nombres, le résultat est :

• positif s’il y a un nombre pair de signes négatifs,
• négatif s’il y a un nombre impair de signes négatifs.

Exemple :

(−2) × (−3) × (−4)

= (−2×−3) × −4

= (+6) × −4

= −24

Il y a 3 signes négatifs (nombre impair) → résultat négatif.