L’accompagnement à la résolution de problèmes mathématiques à l’école
L’accompagnement à la résolution de problèmes mathématiques à l’école
Armelle Géninet est professeure de mathématiques et spécialisée en gestion mentale. Elle expose dans son livre Faites les réussir en maths une stratégie pour analyser et comprendre les énoncés de problèmes mathématiques simples. La stratégie qu’elle décrit tient compte des apports de la gestion mentale pour la résolution des problèmes mathématiques.
Difficultés rencontrées dans la résolution de problèmes mathématiques
Les difficultés dans la résolution des problèmes sont à envisager de plusieurs points de vue :
- attention accordée aux différents indices de l’énoncé,
- compréhension du langage écrit, en français, dans la lecture de l’énoncé,
- compréhension du sens des opérations,
- réflexion en lien avec les acquis pour le choix des opérations à faire.
Souvent, les enfants (et les adolescents) ont tendance à se précipiter dans un geste mental de réflexion avant même d’avoir vérifié leur bonne compréhension de l’énoncé. La simple mention du mot “problème” et d’une question provoque une sorte de réflexe : “il faut faire une opération !”
Les prérequis pour résoudre des problèmes
Pour Armelle Géninet, la bonne maîtrise de prérequis est indispensable pour une réflexion efficace relative aux problèmes mathématiques :
- la structure logique des quatre opérations
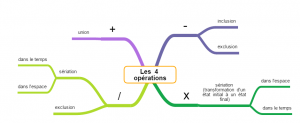
apprendre-reviser-memoriser.fr
- les calculs en complémentarité (d’une part, additions et soustractions sont complémentaires pour passer d’un nombre à un autre; d’autre part, multiplications et soustractions sont complémentaires)
- les liens logiques dans les structures d’énoncés
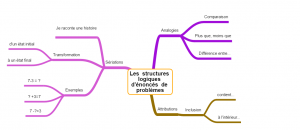
apprendre-reviser-memoriser.fr
Etapes pour pouvoir réfléchir aux énoncés des problèmes mathématiques
- Annoncer aux enfants que le but de l’activité est de se créer une “boîte à outils” qui permette de résoudre tous les problèmes de mathématiques
- Faire vivre aux élèves la compréhension d’un énoncé concret (fort simple et sans difficulté lexicale)
- Mener un dialogue pédagogique avec les enfants pour qu’ils expriment leur vécu dans les évocations concrètes qu’ils se font de l’énoncé
- Donner à résoudre 2 ou 3 problèmes similaires, en augmentant progressivement le niveau linguistique
- Faire rechercher des similitudes et différences entre ces énoncés
- Mettre en évidence la structure logique commune aux différents problèmes posés (analogie, attribution ou sériation spatiotemorelle)
- Choisir un énoncé qui relève de la même logique, mais dont la question amène un nécessaire changement de point de vue
- Mener des dialogues afin que les enfants verbalisent leurs découvertes à chaque étape, anticipent petit à petit d’autres possibles et peut-être même inventent des énoncés de même structure
- Proposer alors un énoncé, puis plusieurs de structure logique différente pour créer un “conflit cognitif” et accompagner les élèves dans la découverte d’une autre structure logique
- Poursuivre ainsi, lentement, sans précipitation, jusqu’à ce que les structures soient mises à jour
……………………………………………………………………………………………………………………………………………….
Source : Faites-les réussir en maths : De l’école à l’entrée au lycée d’Armelle Géninet (éditions Chronique Sociale). Disponible en médiathèque, en librairie ou sur les sites de ecommerce.



