Construire le sens de la division avec les bâtonnets numériques : combien de fois un nombre dans un nombre plus grand ?

Pour effectuer une division, il faut se demander combien de fois il y a un nombre dans un autre.

Les bâtonnets numériques peuvent être utiles pour comprendre cette notion. L’utilisation des bâtonnets numériques s’appuie sur une représentation physique des nombres et des manipulations mathématiques que les enfants vont faire. On expliquera aux enfants que chaque bâtonnet a une valeur : cela signifie que chaque couleur correspond à un nombre.

 

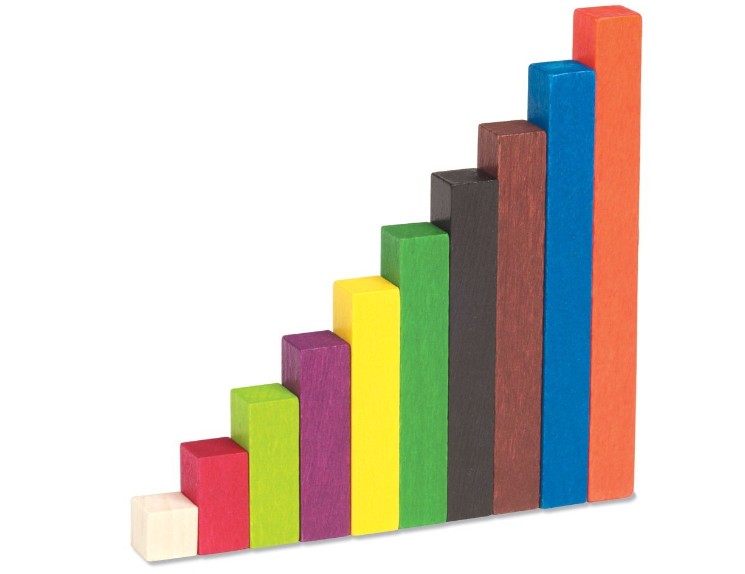
Le carré blanc correspond à 1; les autres bâtonnets sont de forme rectangulaire dont les valeurs sont affichées ci-dessous.

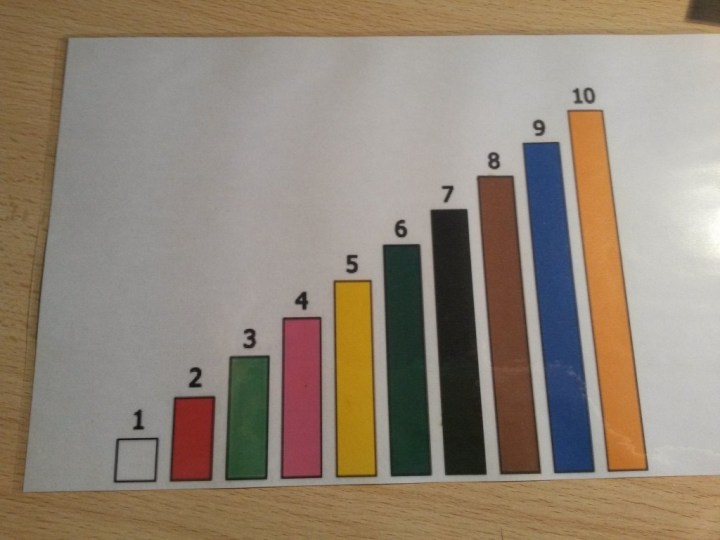
Il est possible de laisser les enfants manipuler les bâtonnets librement dans un premier temps. Ils pourront ainsi commencer à poser des bâtonnets de couleurs différentes les uns à côté des autres et comprendre que des nombres peuvent être décomposés en d’autres nombres.

Par exemple, les enfants pourront comprendre que 6 (bâtonnet vert foncé), c’est 4 fois 1 (carré blanc) + 2 (bâtonnet rouge) ou encore que 6, c’est 2 fois 3 (bâtonnet vert clair).

Une fois que les enfants se seront familiarisé avec les bâtonnets, on leur fournira une aide-mémoire avec les valeurs de chaque bâtonnet. Puis on leur demandera de choisir un nombre pair entre 4 et 10 (4, 6, 8 ou 10).

On leur passera la consigne suivante : placer plusieurs bâtonnets exactement de même couleur les uns à côté des autres pour obtenir la même longueur que le bâtonnet choisi. Si ce n’est pas clair, on leur fera la démonstration avec 2 (bâtonnet rouge) : dans 2, on peut mettre deux fois 1 (deux bâtonnets de couleur blanche qui valent 1 ont la même longueur qu’un bâtonnet rouge de valeur 2).

On laissera les enfants manipuler les bâtonnets en s’exerçant avec tous les nombres pairs : 4 (rose), 6 (vert foncé), 8 (marron) et 10 (bleu). Ils constateront par exemple qu’on peut mettre 2 fois 3 (deux bâtonnets vert clair) ou 3 fois 2 (trois bâtonnets rouges) dans 6 (bâtonnet vert foncé). On fera verbaliser tous les constats que les enfants font à partir des bâtonnets représentant des nombres pairs.

On pourra recommencer avec le bâtonnet de valeur 9 (bleu) : combien de bâtonnets exactement de même couleur peut-on mettre dans 9 pour qu’ils aient la même longueur ? Les enfants constateront qu’il faut 3 bâtonnets de valeur 3 (vert clair) pour obtenir 9 (même longueur).

On pourra ensuite introduire la notion de reste en faisant travailler les enfants sur cette question : combien de bâtonnets exactement de même couleur peut-on mettre dans 7 ? A force de manipulation, les enfants se rendront compte qu’on ne peut pas tomber exactement sur la même longueur que 7 (bâtonnet noir) avec seulement des bâtonnets de même longueur. On leur demandera alors de se rapprocher au maximum de la longueur en utilisant un carré blanc de valeur 1 pour compléter. Les enfants se rendront compte que 7, c’est 2 fois 3 + 1 ou 3 fois 2 +1.

On pourra ensuite leur proposer des manipulations plus directives :

• combien de fois 3 (bâtonnet vert clair) dans 6 (bâtonnet vert foncé) ? Il faut 2 bâtonnets de 3 pour faire 6. Dans 6, il y a 2 fois 3.
• combien de fois 3 (bâtonnet vert clair) dans 9 (bâtonnet bleu) ? Il faut 3 bâtonnets de 3 pour faire 9. Dans 9, il y a 3 fois 3.
• combien de fois 3 (bâtonnet vert clair) dans 7 (bâtonnet noir) ? Il faut 2 bâtonnets de 3 et 1 bâtonnet de 1 pour faire 7. Dans 7, il y a 2 fois 3 +1. 1 est le reste.
• combien de fois 3 (bâtonnet vert clair) dans 8 (bâtonnet marron ? Il faut 2 bâtonnets de 3 et 2 bâtonnets de 1 pour faire 8. Dans 8, il y a 2 fois 3 +2. 2 est le reste.
• combien de fois 3 (bâtonnet vert clair) dans 10 (bâtonnet orange) ?  Il faut 3 bâtonnets de 3 et 1 bâtonnet de 1 pour faire 9. Dans 9, il y a 3 fois 3 +1. 1 est le reste.

On conclura que diviser un nombre par 3, c’est chercher combien de fois il y a 3 dans ce nombre. Parfois, il y a un reste.

On pourra compléter l’entraînement avec d’autres nombres :

• combien de fois 4 (bâtonnet rose) dans 5 (bâtonnet jaune) ?
• combien de fois 4 (bâtonnet rose) dans 6 (bâtonnet vert foncé) ?
• combien de fois 4 (bâtonnet rose) dans 7 (bâtonnet noir) ?
• combien de fois 4 (bâtonnet rose) dans 8 (bâtonnet marron ?
• combien de fois 4 (bâtonnet rose) dans 9 (bâtonnet bleu) ?
• combien de fois 4 (bâtonnet rose) dans 10 (bâtonnet orange) ?

On conclura que diviser un nombre par 4, c’est chercher combien de fois il y a 4 dans ce nombre. Parfois, il y a un reste.

D’autres manipulations pourront être effectuées avec d’autres nombres, y compris avec des nombres supérieurs à dix (il faudra alors accoler des réglettes à celle orange de valeur 10).

…………………………………

Les bâtonnets numériques sont disponibles en centres culturels, en magasins de jouets ou sur internet.