Géométrie : carte mentale des axes de symétrie des polygones usuels
Géométrie : carte mentale des axes de symétrie des polygones usuels
Je vous propose une carte mentale qui reprend les axes de symétrie des polygones usuels : rectangle, losange, carré, triangle équilatéral et triangle isocèle. On peut remarquer que les carrés sont à la fois des losanges et des rectangles, si bien qu’ils ont 4 axes de symétrie :
- les médiatrices de ses côtés (comme les rectangles),
- les droites qui portent les diagonales (comme les losanges).
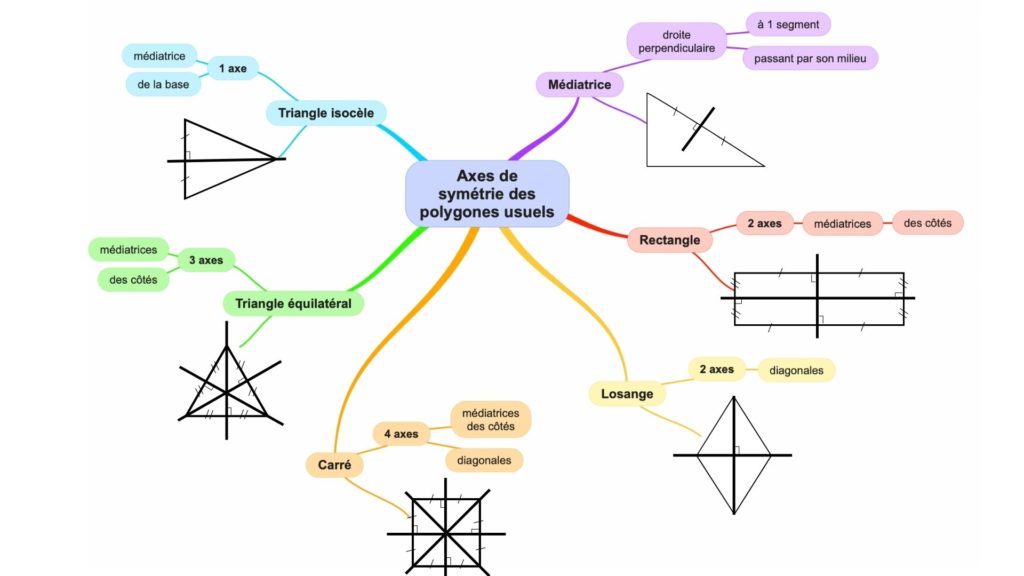
Télécharger la carte mentale des axes de symétrie des polygones au format PDF pour impression
En géométrie, un axe de symétrie d’une figure est une droite qui partage cette figure en deux parties superposables par pliage (ou par réflexion). Pour qu’une droite soit un axe de symétrie, elle doit vérifier deux conditions :
- Diviser la figure en deux moitiés : La droite “coupe” la figure en deux parties identiques en forme et en taille.
- Superposition par réflexion : Si on plie la figure le long de l’axe, les deux parties se superposent parfaitement (comme un miroir). Exemple : Pour un cœur, l’axe vertical le divise en deux moitiés symétriques.
Rectangle : Les axes passent par les milieux des côtés opposés (vertical et horizontal). Il y en a 2.
Losange : Les axes sont les diagonales du losange. Il y en a 2.
Carré : 2 diagonales + 2 axes passant par les milieux des côtés opposés. Il y en a 4.
Triangle équilatéral : Chaque axe passe par un sommet et le milieu du côté opposé. Il y en a 3.
Triangle isocèle : L’axe passe par le sommet principal et le milieu de la base. Il y en a 1.
Comment le vérifier ?
Méthode du pliage : Si tu plies la figure le long de la droite et que les bords coïncident, c’est un axe de symétrie.
Méthode du miroir : Place un miroir le long de la droite – si la figure semble complète dans le reflet, c’est un axe.
Méthode des points : Pour chaque point d’un côté de l’axe, son symétrique (à la même distance de l’axe) doit exister dans l’autre moitié.
……………………………………
Plus de ressources pour la géométrie en cycle 3 (CM1/ CM2 et sixième) :



