Carte mentale des calculs avec les fractions (addition, soustraction, multiplication, division)
Carte mentale des calculs avec les fractions (addition, soustraction, multiplication, division)
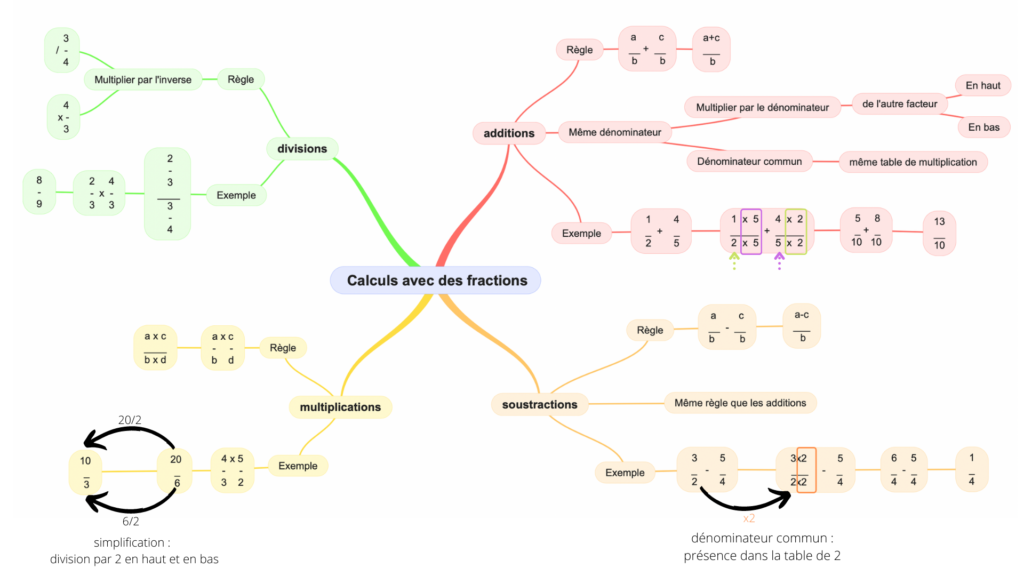
Je vous propose une carte mentale des calculs avec les fractions (addition, soustraction, multiplication, division). Cette carte peut servir de sous-main ou aide mémoire pour les élèves au collège.
Télécharger la carte mentale des calculs avec des fractions au format PDF pour l’imprimer
Additions
Règle : a/b + c/b = (a+c)/b
Mettre sur le même dénominateur : multiplier par le dénominateur de l’autre facteur en haut et en bas
Exemple : 1/2 + 4/5 = (1×5)/(2×5) + (4×2)/5×2) = 5/10 + 8/10 = 13/10
Soustractions
Règle : a/b – c/b = (a-c)/b
Mettre sur le même dénominateur : multiplier par le dénominateur de l’autre facteur en haut et en bas
Exemple : 3/2 – 5/4 = (3×2)/(2×2) – (5/4) = 6/4 – 5/4 = 1/4
Multiplications
Règle : (a/b)x(c/d) = (axc)/ (bxd)
Exemple : 4/3 x 5/2 = 20/6
Divisions
Règle : multiplier par l’inverse
Exemple : (2/3)/(3/4) = 2/3 x 4/3 = 8/9
Comment enseigner les opérations ?
Addition et soustraction
Commencer par des fractions de même dénominateur (ex : ¼ + ¾ =
4⁄4
), en illustrant le regroupement de parts d’un même tout.
Introduire ensuite les fractions de dénominateurs différents, en passant par des manipulations (partager une bande en parts égales, superposer des fractions sur des supports concrets) avant de formaliser la recherche du dénominateur commun.
Multiplication
Présenter la multiplication comme « prendre une fraction d’une fraction » (ex : 2/3 x 3/4), en utilisant des surfaces ou des découpages (partager un rectangle en 3, puis prendre les 2/3, puis partager chaque tiers en 4).
Mettre en évidence la règle du produit des numérateurs et des dénominateurs après plusieurs manipulations concrètes.
Division
Introduire la division par une fraction comme la recherche du nombre de fois qu’une fraction est contenue dans une autre (exemple : combien de quarts dans trois demi ?)
Utiliser des exemples concrets (partager des objets, des longueurs) et des schémas pour illustrer le sens de la division.
Formaliser ensuite la règle « multiplier par l’inverse » après avoir compris le sens de l’opération.
………………………………………….
D’autres ressources pour calculer avec des fractions :
Fiche synthèse sur les propriétés des additions et des soustractions de fractions



