Démontrer en géométrie : méthodologie pour la démonstration

Je vous propose un outil pour aider les enfants à suivre les étapes de la méthode pour démontrer en géométrie au collège. Le rappel des étapes dans l’ordre permet d’ancrer la méthodologie pour les démonstrations en géométrie. La forme en accordéon permet de déplier chaque étape l’une après l’autre dans une démarche méthodologique pas à pas. L’idée est de disposer d’un gabarit à remplir bien précis (à utiliser avec toutes les propriétés et les formules d’aire, de périmètre ou de volume qui nécessitent d’être apprises par coeur).

Une fois imprimé, le livret pourra être plié comme un accordéon afin de former une sorte d’accordéon où chaque page propose une étape de la méthode de démonstration en géométrie.

Démontrer en géométrie suppose de savoir identifier les éléments connus et les éléments à chercher. Cela peut passer par un code couleur : surligner en jaune les éléments connus et utiles de l’énoncé, surligner en vert ce qu’on cherche (soit dans le texte de l’énoncé, soit directement sur la figure géométrique). 

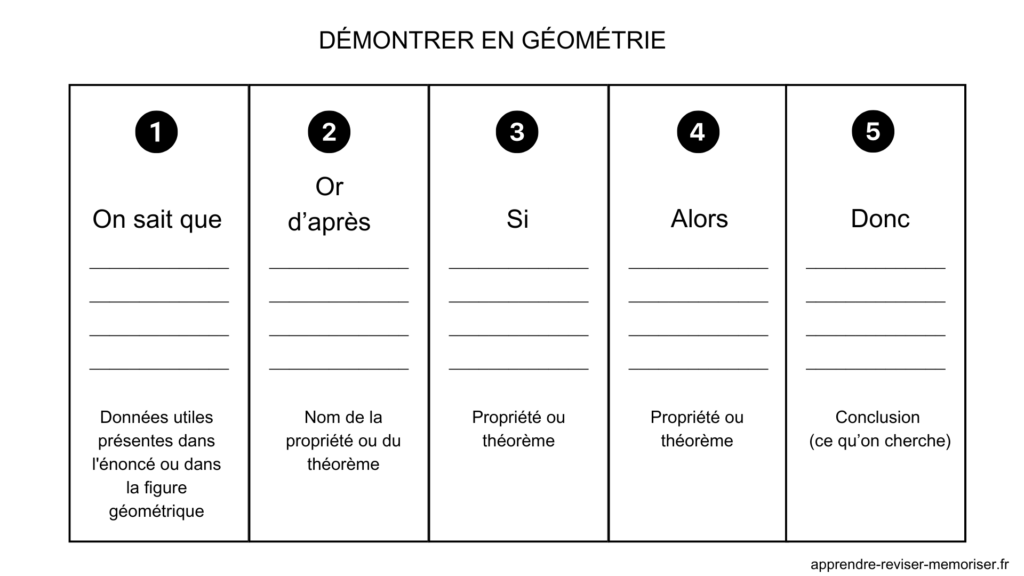
Télécharger la méthodologie pour démontrer en géométrie au format PDF pour l’imprimer

Étape 1 : On sait que

Ce sont les données utiles présentes dans l’énoncé ou dans la figure géométrique.

Étape 2 : Or d’après

On note le nom de la propriété ou du théorème de géométrie.

Étape 3 : Si

Étape 4 :  Alors

Étape 5 : Donc

C’est la conclusion (ce qu’on cherche)

 

Par exemple, pour démontrer que deux droites sont parallèles : 

1.On sait que d1 est parallèle à d3 et d2 est parallèle à d3

2.Or d’après la propriété géométrique de la troisième droite parallèle,

3.Si deux droites sont parallèles à une même troisième,

4.Alors elles sont parallèles entre elles.

5.Donc les deux droites d1 et d2 sont parallèles.