Comment bien expliquer une leçon à son enfant ?
Comment bien expliquer une leçon à son enfant ?

Au moment des devoirs, de nombreux parents se demandent comment bien expliquer une leçon aux enfants. Il arrive souvent qu’un enfant dise qu’il n’a pas compris et qu’il n’arrive ni à apprendre la leçon ni à résoudre les exercices d’application. Il n’existe pas une seule manière de bien expliquer une leçon à un enfant car cela dépend de la matière, de la classe de l’enfant, de son niveau de maîtrise des prérequis ou encore de son profil (est-il porteur d’un trouble de l’apprentissage ou d’un trouble neurodéveloppemental ?)
Un élément essentiel à garder en tête est que l’objectif des devoirs ne devrait jamais être de simplement relire une leçon. Comprendre et mémoriser ne sont pas synonymes de relire. Apprendre, c’est se poser des questions en s’autoévaluant sans avoir la leçon sous les yeux.
Les relectures faisant suite à une première séance de devoirs doivent se faire avec un objectif en tête :
- chercher des explications sur une notion non comprise,
- chercher des images pour illustrer telle ou telle notion,
- repérer la trame du cours/ chercher un plan logique,
- connecter les informations qui ont des liens entre elles.
Les relectures peuvent porter sur des passages précis, pas forcément sur tout le cours.
Il existe toutefois des stratégies qui peuvent être adaptées au contenu. Voici 9 stratégies détaillées et illustrées pour expliquer une leçon à un enfant.
1.Vérifier les prérequis
Une question utile à poser aux enfants pour savoir s’ils ont compris une leçon est simplement : Qu’as-tu compris ? L’enfant devra alors expliquer et reformuler avec ses propres mots, trouver ses propres exemples, faire des liens avec des informations déjà connues. La compréhension est au cœur de l’activité intellectuelle car il s’agit de découvrir des rapports entre des éléments et d’en inventer de nouveaux. C’est à partir de ces éléments qu’on peut identifier les points de blocage que nous devrons expliquer aux enfants :
- Y a-t-il un mot inconnu qui empêche de comprendre un cours ? Dans ce cas, un dictionnaire ou une référence à un cours précédent sera utile.
- Y a-t-il trop d’informations d’un coup, ce qui entraîne une surcharge et des confusions ? Dans ce cas, il est possible de fractionner les éléments à apprendre en y allant pas à pas. Il faut sélectionner ce qui est pertinent : quelles sont les informations indispensables (comme les mots clés, les définitions, les dates, les théorèmes) ? quelles sont les informations secondaires dont la maîtrise n’est pas essentielle pour comprendre ?
- Y a-t-il des connaissances prérequises non maîtrisées (comme si les fondations d’une maison étaient trop fragiles) ? Dans ce cas, il faut reprendre les leçons précédentes et expliquer les notions qui auraient dû être déjà maîtrisées (par exemple, maîtriser les puissances en mathématiques nécessite de connaître les tables de multiplication). Des exercices d’entraînement faits en classe ou bien les années précédentes pourront être refaits afin d’assurer la maîtrise des prérequis.
2.Utiliser des couleurs
Voici un exemple d’utilisation de couleurs, combinée à la narration et au jeu, pour expliquer le théorème de Thalès. Cette vidéo est proposée par Jacqueline Felzines, sur la page de son association Dys sur Dys. Cette page Facebook est une mine d’or à consulter absolument pour savoir comment expliquer une leçon aux enfants, dans toutes les matières et pour tous les niveaux (de l’élémentaire au collège). Jacqueline Felzines travaille avec des enfants et des collégiens atteints de troubles de l’apprentissage, mais les stratégies qu’elle développe sont utilisables par tous les élèves.
3.Faire des liens, des métaphores, des catégories
Expliquer une leçon, c’est permettre aux enfants de comprendre. Passer par des comparaisons ou des métaphores aide les enfants car cela permet de relier les nouvelles notions à des choses qu’ils ont déjà en tête.
Par exemple, le plasma est comme un fleuve, et les différentes cellules sanguines sont des bateaux qui flottent dans le courant.
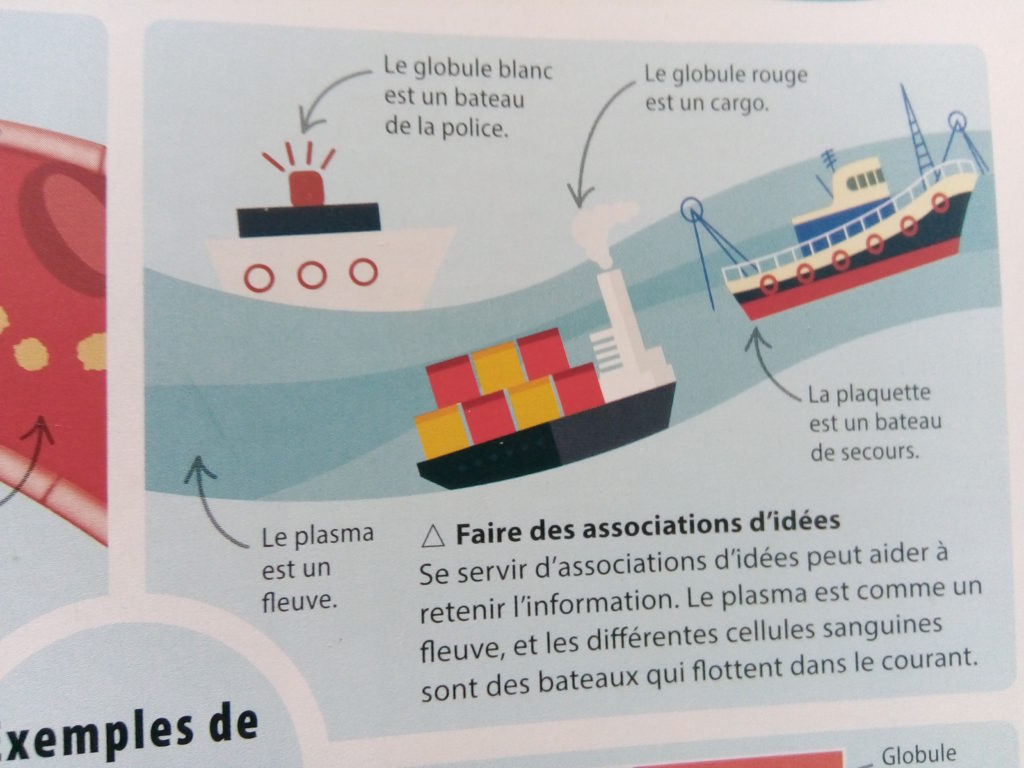
Source : Aidez votre ado à apprendre: 80 techniques pédagogiques positives en images de Carol Vorderman (éditions Eyrolles)
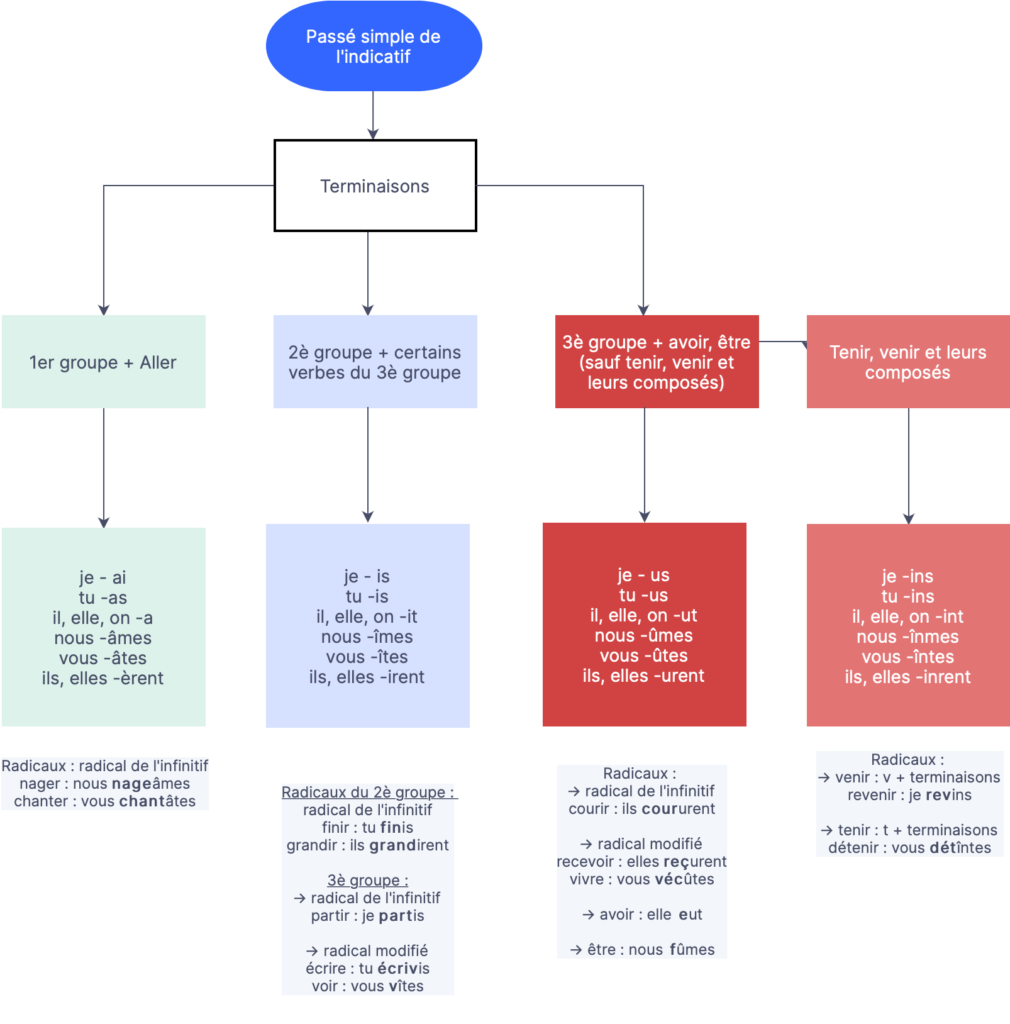
Faire des catégories, c’est faire des groupes d’éléments ayant des points communs. Par exemple, il est possible de repérer les régularités dans les terminaisons des verbes pour mémoriser la conjugaison. Je vous propose un exemple ci-dessous pour les terminaisons des verbes conjugués au présent de l’indicatif.

Un autre exemple de regroupement des régularités dans des catégories avec le passé simple de l’indicatif. :
4.Modifier le contenu pour savoir comment bien expliquer une leçon
Il est utile d‘agir sur le contenu d’une leçon pour la comprendre. Pour expliquer une leçon à un enfant, on peut l’inviter à transformer le texte écrit en schéma, en enregistrement oral, en dessin ou en carte mentale.
Il est également recommandé de repérer les informations importantes et de créer des cartes questions/ réponses : au recto, le mot à savoir définir; au verso, la définition. Les enfants pourront piocher une carte et lire le recto, répondre, puis se corriger avec le verso. C’est le principe des flash cards.
Il est possible de créer des fiches de révisions avec seulement les titres et sous-titres d’une leçon qu’il faudra compléter à l’oral.
5.Expliciter les mots clés (verbes, pronom interrogatif, mots de liaison)
Expliquer, c’est transmettre des stratégies de résolution. Par exemple : « Dans la question, Qui est le président de la France ?, je cherche le mot interrogatif. C’est “qui”. Qui désigne une personne donc je cherche un nom propre. »
Lever les implicites dans les activités d’apprentissage scolaires est essentiel car les élèves ne savent pas toujours :
- quel est l’objectif véritable de la tâche (pourquoi l’enseignant donne cette activité),
- quelles sont les attentes de l’enseignant (ce qu’il a en tête en termes de procédure et de résultat),
- à quoi faire attention,
- comment s’y prendre,
- comment savoir quand c’est fini,
- comment savoir quand c’est réussi.
L’idée est de rendre claires les règles du jeu pour que le chemin à suivre soit connu et compris par tous les élèves. Il ne suffit pas de demander à un élève de reformuler la consigne avec ses propres mots, mais il sera plus efficace de lui demander :
- “Qu’est-ce que tu as compris ?”
- “A quoi vas-tu faire attention ?”
- “Comment vas-tu t’y prendre pour réussir ?”
- “Quelle est la première étape ? Et ensuite ? Quand t’arrêteras-tu ?”
6.Procéder par étape : STOP + résumés intermédiaires
Expliquer une leçon à un enfant, c’est aussi l’habituer à s’arrêter à chaque paragraphe et à effectuer des résumés intermédiaires. Il peut passer par un code couleur pour surligner les élément qui se rapportent à une même idée de la même couleur. Puis on lui demandera : qu’est-ce que tu viens de lire ? comment peux-tu le résumer avec tes mots ou le dessiner ?
Au fur et à mesure, l’enfant doit prendre l’habitude de se poser des questions tout seul sur ce qu’il vient de lire : se forcer à élaborer des questions amorce le processus de compréhension. Cela peut passer par des questions ouvertes : qui ? quoi ? où ? quand ? pourquoi ?
L’enfant a toujours le droit d’effectuer des retours en arrière dans sa leçon (pour revenir, par exemple, sur des passages lus antérieurement et susceptibles d’être à l’origine des difficultés à cause de mots inconnus). Le moment des devoirs n’est pas le moment de l’évaluation donc l’enfant a le droit de s’aider, de recommencer, de faire des aller-retours.
7.Passer par le jeu pour bien expliquer une leçon
Reformuler les consignes sous forme de jeux ou de défis. Par exemple :
- on mène l’enquête,
- mission pour super héros,
- cap ou pas cap,
- le premier qui trouve
8.Contourner les difficultés de mémorisation avec des astuces
Des astuces de mémorisation permettent de contourner les difficultés quand “ça ne veut pas rentrer”. Je vous propose des exemples avec les tables de multiplication à apprendre par coeur.
- Astuces sur les doigts : la table de 9 sur les doigts
-
- Mettre les deux mains face à soi, paumes visibles (le pouce gauche se retrouve à l’extrémité gauche et le pouce droit à l’extrémité droite).
- Baisser le doigt qui correspond au multiplicateur en comptant les doigts à partir du pouce gauche.
- Compter le nombre de doigts avant le doigt baissé : ce nombre représente le chiffre de dizaines du résultat.
- Compter le nombre de doigts après le doigt baissé: ce nombre représente le chiffre des unités du résultat.
Exemples :
->Pour trouver le résultat de 9×4, baisser le quatrième doigt en partant du pouce gauche (l’annulaire de la main gauche sera baissé).
Compter le nombre de doigts avant le doigt baissé (ici 3) : le résultat aura 3 dizaines.
Compter le nombre de doigts après le doigt baissé (ici 6) : le résultat aura 6 unités.
Lire le résultat de 9×4: 3 dizaines et 6 unités donc 9×4=36.
->Pour trouver le résultat de 9×8, baisser le huitième doigt en partant du pouce gauche (le majeur de la main droite sera baissé).
Compter le nombre de doigts avant le doigt baissé (ici 7) : le résultat aura 7 dizaines.
Compter le nombre de doigts après le doigt baissé (ici 2) : le résultat aura 2 unités.
Lire le résultat de 9×8 : 7 dizaines et 2 unités donc 9×8=72.
- Les images mentales : les Multimalins
Les cartes Multimalin, créées par Mathieu Protin (professeur des écoles), sont basées sur le principe de la visualisation mentale. La méthode Multimalin propose de transformer les chiffres en objets ou en personnages puis de raconter une histoire avec ces objets ou ces personnages.



- Des astuces mnémotechniques sans devoir apprendre par coeur
Il existe des astuces pour retrouver les tables de multiplication, comme la table de 8 de haut en bas :
- de haut en bas, écrire les nombre de 0 à 8 les uns sous les autres en doublant le 4 (on écrit donc deux fois le nombre 4 l’un sous l’autre et on peut se rappeler de l’écrire deux fois parce que 2×4=8 et qu’on cherche les résultats de la table de 8)
- de bas en haut, face à la colonne de nombre formée précédemment, écrire les nombres de 0 à 8 de 2 en 2 (0, 2, 4, 6,8, 0, 2, 4, 6, 8).
On aura ainsi tous les résultats de la table de 8 écrits dans l’ordre de 8×1 à 8×10.

9.S’entraîner pour comprendre
C’est à force de s’entraîner, de s’exercer et de pratiquer qu’on intègre les règles. Cela veut dire que la mémorisation entre en jeu dans la compréhension. Plus on possède d’acquis en mémoire, plus on est capable de comprendre. Le nombre de tests via des exercices compte plus dans la mémorisation que le nombre d’heures passées à étudier.
Pour se rappeler de façon durable, il faut élaborer des stratégies de mémorisation, car comprendre ne suffit pas pour mémoriser. De même, mémoriser ne suffit pas pour comprendre.
Il est important de garder en tête que le processus d’acquisition des connaissances s’effectue au fil de trois grandes étapes directrices :
- d’abord la compréhension de la notion,
- puis la pratique
- enfin, la révision.
Il ne faut pas s’arrêter à la première étape : celle de la compréhension. Même quand on a compris, faire des exercices et réviser les théorèmes ou les formules mathématiques demeure indispensable.



