Carte mentale des nombres premiers (collège)

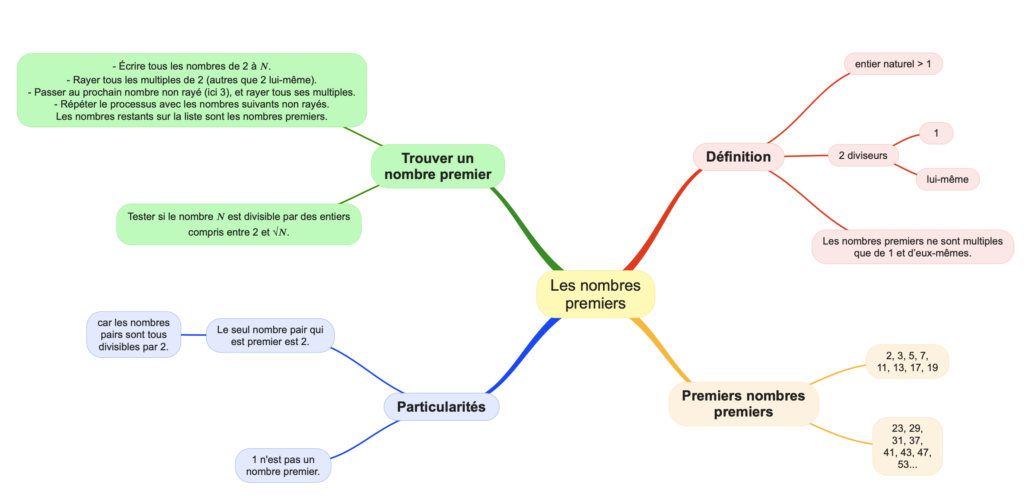
Pour aider les collégiens, je vous propose une carte mentale des nombres premiers.

Pour identifier les nombres premiers, il est essentiel de comprendre certains concepts mathématiques fondamentaux et d’utiliser quelques techniques efficaces. Voici les éléments importants à connaître.

1. Définition d’un nombre premier

Un nombre premier est un entier naturel supérieur à 1 qui n’a que deux diviseurs : 1 et lui-même. En d’autres termes, un nombre premier ne peut pas être divisé exactement par un autre nombre entier que 1 et lui-même.

2. Les premiers nombres premiers

Il est utile de connaître les premiers nombres premiers, car cela facilite le processus de vérification pour d’autres nombres. Les plus petits nombres premiers sont : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53…

3. Le seul nombre premier pair

Le seul nombre pair qui est premier est 2. Tous les autres nombres premiers sont impairs, car les nombres pairs sont divisibles par 2.

4. Divisibilité

Pour déterminer si un nombre est premier, il faut vérifier s’il n’est pas divisible par les nombres premiers inférieurs ou égaux à √. Si aucun de ces nombres ne le divise, alors est premier.

Pour identifier ou trouver des nombres premiers, il faut comprendre la définition, utiliser des méthodes comme la division directe ou le crible d’Ératosthène, et connaître des propriétés liées à la divisibilité et aux racines carrées.

>> Télécharger la carte mentale des nombres premiers au format PDF pour l’imprimer.

Pour aller plus loin sur les nombres premiers : une activité pour en construire le sens.