Comprendre la notion de racine carrée
Comprendre la notion de racine carrée : présentation avec la méthode Lyons pour une compréhension effective à travers la manipulation
Dans la méthode Lyons, les frères Robert et Michel Lyons estiment qu’on peut aborder la notion de racine carrée dès 6 ans.
Le travail avec du matériel simple et concret permet d’attribuer à une opération, telle extraire la racine carrée, son sens véritable qui est à la portée de tout élève de six ans.
Je vous propose leur démarche pour permettre aux élèves de comprendre la notion de racine carrée :
Problème 1
Demandez à l’élève ce qu’est un rectangle.
Demandez-lui de vous montrer des objets où il peut observer un rectangle.
Discutez avec lui de ce qu’est un rectangle en vous assurant de faire ressortir que le rectangle :
- possède exactement quatre coins,
- et que ces quatre coins sont identiques (comme les coins d’une feuille de papier ) .
Montrez maintenant quelques carrés et demandez-lui si ce sont des rectangles.
Les élèves doivent trouver que tous les carrés sont des rectangles car ils ont exactement quatre angles droits.
En fait, ce sont des « rectangles améliorés », c’est-à-dire des rectangles qui doivent respecter une condition supplémentaire : posséder quatre côtés de même longueur. Ainsi, tous les carrés sont des rectangles alors que certains rectangles sont des carrés.
Problème 2
Dans les problèmes qui suivent, au besoin, rappelez à l’élève ce qu’est un carré et ce qu’est un rectangle.
Matériel : 30 cubes carrées d’environ 1 cm à 2 cm de côté (pour ma part, j’ai utilisé des bâtonnets numériques qui valent une unité).
Enoncé : Avec 9 tuiles ( ou cubes ), nous pouvons recouvrir un plancher qui a la forme d’un carré. Construis ce plancher.

Source : http://www.defimath.ca/ecole-maison/volume1/vol.1ch.5.pdf
Certains élèves se contentent de faire le tour du carré, ne plaçant aucune pièce au centre et n’utilisant ainsi que huit pièces. Si l’élève agit ainsi, dites-lui que ce plancher est bien dangereux avec un trou au centre, qu’il faut combler ce trou.
On dit que 9 est un nombre carré, pourquoi ? ( Avec 9 pièces, on peut faire un carré. )
Problème 3
Peux-tu faire un carré qui soit juste un peu plus grand que celui-là ? ( Oui , avec 16 pièces) .
Peux-tu en faire un autre qui soit encore un peu plus grand ? ( Oui, avec 25 pièces. )
Certains élèves font régulièrement un rectangle, tel le suivant, au lieu d’un carré :
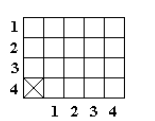
Source : http://www.defimath.ca/ecole-maison/volume1/vol.1ch.5.pdf
Quand vous leur demandez si les côtés sont tous égaux, ils les comptent tel qu’illustré en ne comptant qu’une fois le carré du coin marqué d’un X. En fait, ils ont encore de la difficulté à comprendre qu’un élément puisse appartenir en même temps à deux ensembles distincts.
Il faut créer un conflit cognitif ( ça ne fait pas mal ! ) de la façon suivante :
Nous allons vérifier. Commence cette fois en comptant les pièces du haut. Il en trouvera cinq.
Montrez votre étonnement et demandez-lui de dénombrer les pièces de droite. Il risque de n’en trouver que trois s’il répète son erreur originale. Étonnez-vous encore une fois : « Comment se fait-il que cela ne donne pas toujours quatre ? » Laissez l’élève réfléchir à ce problème. Évitez de lui expliquer comment résoudre cette difficulté. Il doit y parvenir seul, quitte à laisser le problème de côté pour l’instant et à y revenir dans quelques jours.
Contentez-vous donc de bien faire ressortir le problème posé par le dénombrement des bords du carré.
Problème 4
Nous savons que les nombres 9, 16 et 25 sont des carrés.
Quelle est la longueur du côté d’un carré de 25 pièces ? (5 pièces )
Et maintenant, quelle est la longueur du côté d’un carré de 9 pièces ? ( 3 pièces )
Bon, c’est un peu long de répéter chaque fois « Quelle est la longueur du côté d’un carré de 9 ou de 25 pièces ? » Désormais, je vais l’écrire comme ceci √9 ou √25.
Ce signe, est un symbole secret qu’utilisent les grands mathématiciens pour dire « Quelle est la longueur du côté d’un carré qui a 9 ou 25 pièces ? »
Voyons maintenant si tu peux découvrir ce que les grands mathématiciens veulent dire lorsqu’ils écrivent : √9, √4, √1 ? ( 3, 2, 1 ).
(Les élèves ont le droit de manipuler les cubes)
………………………………………………………………………………………………
Pour découvrir (et télécharger) la méthode Lyons au complet : www.defimath.ca/ecole-maison




